また,割合を表す 01,001 をそれぞれ 1 割,1 分(ぶ)といいます。 (例) 2 割 → 02 → 2 10 = 1 5 ⎞ ⎠ 2 割 5 分 → 025 → 25 100 = 1 4 ⎞ ⎠ 小数を使うと計算ミスをしやすいので,これから割合を文字式の中で使う 場合は分数に直すようにしましょう。 cmt1b1z1j503元の中でr比で表された割合を分数で表すJと いった問題場面が用意されており,割合に触れる 機会が多く設定されている。この定義の濃いは, 比と割合の指導順序の異なりや,素地指導による 割合の理解度からくるものだと考える。例えば、$75$%は分数に直すと $\dfrac{75}{100}$ になります。必要に応じて約分してください。 関連:約分のやり方と計算ツール ・分子が分母が大きい場合、百分率は $100$ %より大きくなります。例えば、$\dfrac{3}{2}$ をパーセントで表すと、$150$%になります。

印刷可能無料 算数 割合 デザイン文具
割合 を 表す 分数
割合 を 表す 分数-分数にある2つの意味のうち、第一義 ( 1を3等分したものを2つ集めたもの= 2/3 )は3年生で学習します。 ページのプリントでは、第二義 ( 2を3でわったもの= 2/3 )つまり、わり算の商を表すための分数 (商の分数)を中心に、その表し方や計算方法を分数は比や割合といった概念に対応しており、0 でない数 a を分母と分子にそれぞれかけても割っても、その分数の表す数は変わらない。 n m = n × a m × a = n ÷ a m ÷ a ( a ≠ 0 ) {\displaystyle {n \over m}={n\times a \over m\times a}={n\div a \over m\div a}\quad (a\neq 0)}



小学校5年生算数 割合を表すグラフ
中学受験に必要な算数に割合というのがあります。 割合の表し方はいくつかあり、小数、分数、百分率(%)、歩合( 割 分)で表されます。 この割合の公式がなるべく簡単に覚えられる方法を紹介します。 はじめに商村 異分数の意味の多様性とその指導 ③ 量分数 量分数については狭くとらえる立場から広くとらえる立場まで大きく3つに分けることがで きる。 まず、狭くとらえるものは「はんぱの量に依存し、はんぱの量xと単位とのあいだの共通 尺度で、測った測定値Jととらえる立場である。・その11_割合・小数倍の考え方 (1) 5年 割合の表し方・「小数(十進数系)で表す割合とは?」 前回、「割合の表し方には、大きく分けて2種類ある」と記しましたが、今度は見方を変えて、「小数(十進数系)」と「分数系」に分けて考えてみます。
1の左か右に があったら,このわり算! 図を使って「何わる何」の関係を明らかにする。 1の上の数から,1に向けて矢印をかき,「÷数」をそえる。分数は比や割合といった概念に対応しており、0 でない数 a を分母と分子にそれぞれかけても割っても、その分数の表す数は変わらない。 n m = n × a m × a = n ÷ a m ÷ a ( a ≠ 0 ) {\displaystyle {n \over m}={n\times a \over m\times a}={n\div a \over m\div a}\quad (a\neq 0)}例えば、$75$%は分数に直すと $\dfrac{75}{100}$ になります。必要に応じて約分してください。 関連:約分のやり方と計算ツール ・分子が分母が大きい場合、百分率は $100$ %より大きくなります。例えば、$\dfrac{3}{2}$ をパーセントで表すと、$150$%になります。
また,割合を表すのに,歩合 ぶあい を使うこともあります。 割合を表す小数 1 01 001 0001 百分率 100% 10% 1% 01% 歩合 10割 1割 1分 1厘 割合を表したグラフに,「帯グラフ」や「円グラフ」があります。 百分率 ひゃくぶんりつ と歩合 ぶあい チャレンジシート6/18 割合を表す分数の使い方を考え,分数倍 ・ 理解が難しい子どもには「倍」 のを文章題の解き方を考える。 をつけて指導する。 線分図を使って考える。 ・ 関係図を使って,どこが分かれまた,割合を表すのに,歩合 ぶあい を使うこともあります。 割合を表す小数 1 01 001 0001 百分率 100% 10% 1% 01% 歩合 10割 1割 1分 1厘 割合を表したグラフに,「帯グラフ」や「円グラフ」があります。 百分率 ひゃくぶんりつ と歩合 ぶあい チャレンジシート


Http Edu City Shimanto Lg Jp Gudo E App Webroot Files Uploads E7 Ac Ac Ef 92 E5 Ad A6 E5 B9 B4 E7 Ae 97 E6 95 B0 E7 91 E5 Ad A6 E7 Bf 92 E6 8c 87 E5 B0 8e E6 A1 80 8c E5 86 81 91 81 9f E5 81 8d 81 95 92 81 8f 81 9d 81 86 80 8d Pdf


Www1 Iwate School Jp Action Common Download Main Upload Id 1168
分数は比や割合といった概念に対応しており、0 でない数 a を分母と分子にそれぞれかけても割っても、その分数の表す数は変わらない。 n m = n × a m × a = n ÷ a m ÷ a ( a ≠ 0 ) {\displaystyle {n \over m}={n\times a \over m\times a}={n\div a \over m\div a}\quad (a\neq 0)}わり算」や「分数と倍」を学習する。「小数 と倍」と「分数と倍」では,何倍にあたるか を求めているので,これは割合を求める第1 用法へつながっている。「小数と倍」は,教 科書3 第5 学年上p44~45 において扱われ ている。分数、小数で表す2パターンの答え方があるんだけど 自分の好みの方で答えてもらえればokだよ なんでこんな風に表すの? という部分を説明していきますが まず、割合(パーセント)を 分数、小数で表す練習をしておきましょう。 割合を分数、小数で


Www Pref Hiroshima Lg Jp Uploaded Attachment Pdf


Http Www Hiroshima C Ed Jp Web An E San San E 003 Pdf
もくじ 1分数のかけ算 11小数×整数 12小数×小数 2割合を表す分数 3分数と面積、分数と時間 31分数と面積 32分数と割合分数(分割分数) ① 「petボトルから花瓶に水を とる」というのは、実際には1リットルをとることになります。 ①のような分数表現を割合分数または分割分数といいます。この場合は全体の量が決まって始めて目的の量が決まるものですから、相対的な量の表現方法であるといえます。割合分数(分割分数) ① 「petボトルから花瓶に水を とる」というのは、実際には1リットルをとることになります。 ①のような分数表現を割合分数または分割分数といいます。この場合は全体の量が決まって始めて目的の量が決まるものですから、相対的な量の表現方法であるといえます。


Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Zissenmoderu Documents S 053 Pdf



ベストコレクション 割合 を 表す 分数 リタ ベルナル
割合を身近に感じてもらう1時間 5年算数「割合の導入」指導実践の前に 前回の記事でも書きましたが、導入は、身近なものから割合を考えていけることを目標としました。 この授業を経て、教科書の内容に進むつもりです。 では、実践第 6 回のテーマは「 分数の概念と計算方法 」です。 割り算 , 割合 , 比の「 変形 」である「 分数 」についての話です。 今までの「 割り算 , 割合 , 比 」の知識 は、この「 分数 」を理解することで 全てが繋がり、完成します 。 分数は小数とも密接な関わりがあります。学校の分数の計算問題では たいてい全体を1に固定した「割合分数」で計算 することになります。 時々、単位を表すものとして「量分数」が使われることがあります。


Http Ousar Lib Okayama U Ac Jp Files Public 4 Cted 001 037 046 Pdf



小6 算数 小6 11 分数のわり算 割合攻略 Youtube
商村 異分数の意味の多様性とその指導 ③ 量分数 量分数については狭くとらえる立場から広くとらえる立場まで大きく3つに分けることがで きる。 まず、狭くとらえるものは「はんぱの量に依存し、はんぱの量xと単位とのあいだの共通 尺度で、測った測定値Jととらえる立場である。算数 割合の文章題ドリルのページへようこそ 上記のボタンから算数 割合の文章題ドリル(pdfプリント・問題集)がダウンロードできます。個人利用は無料です(家庭以外での配布は有料です)。 プリント内の数字はランダムです。375%を分数で表す方法を教えてください 数学 分数の計算で4〇とかあるじゃないですか 例えば1-3分の10とかだったら、1は3分の3にすればいいじゃないですか。
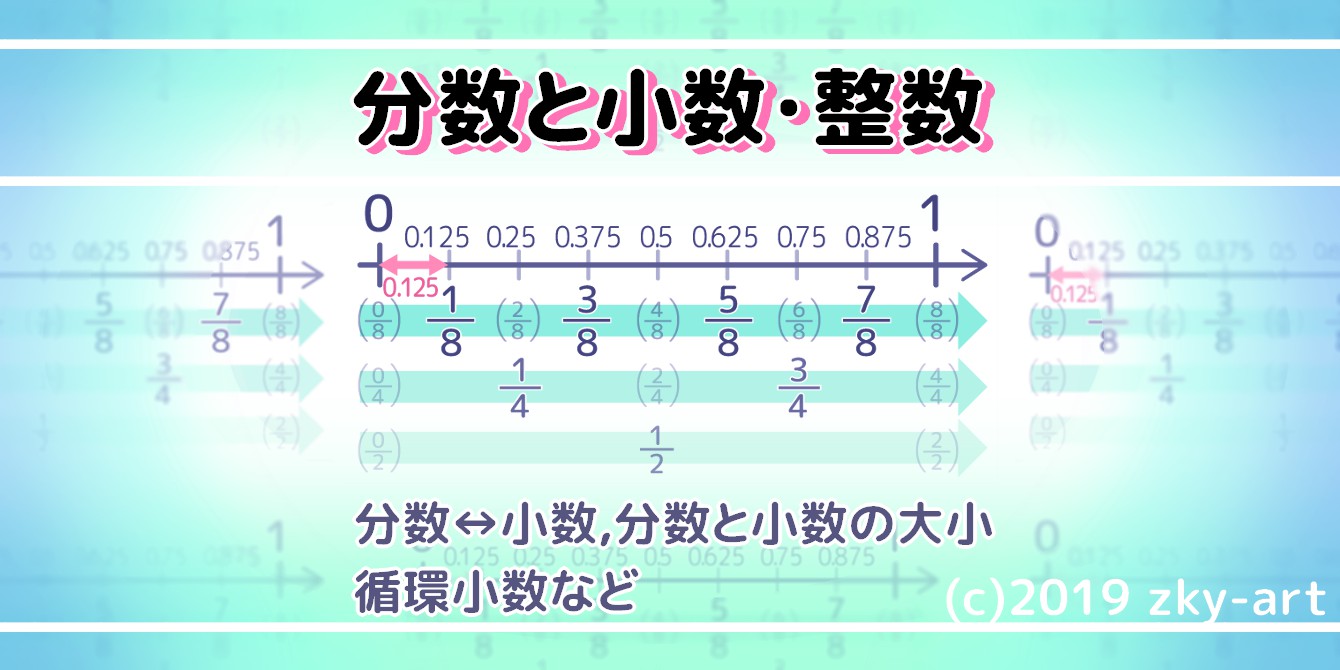


分数を 循環 小数で表す 整数に変換する方法 大小比較の練習問題もあり そうちゃ式 分かりやすい図解算数 旧館


2
分数、小数で表す2パターンの答え方があるんだけど 自分の好みの方で答えてもらえればokだよ なんでこんな風に表すの? という部分を説明していきますが まず、割合(パーセント)を 分数、小数で表す練習をしておきましょう。 割合を分数、小数で小学5年生の算数 わり算と分数|商分数/分数の第二義 練習問題プリント 分数にある2つの意味のうち、第一義 ( 1を3等分したものを2つ集めたもの= 2/3 )は3年生で学習します。分割分数とは「等分割したもののいくつ分を表す数」のこと、割合分数とは「もとになる量を1 と 見たときのくらべる量が何倍になっているかを表す数」のこと、量分数とは「普遍単位の量を a 等


Http Www Educ Pref Fukuoka Jp Html R1 Cm Cm Pdf 54 Pdf


Http Www Dokyoi Pref Hokkaido Lg Jp File Jsp Id
・分数倍を使った問題 ・割合を表す分数の計算の仕方を整数や小数の計算 に関連づけて考えられるようにする。 1 面積の公式をつかって ・長さが分数で表された場合にも面積の公式が使える ことを確かめる。 1小学5年生の算数 割合(割合・比べる量・もとにする量の意味と求め方) 練習問題プリント 教材の新学習指導要領への対応について ただいま、ちびむすドリル小学生では、公開中の教材の 新学習指導要領(年度スタート)への対応 を進めて算数 割合の文章題ドリルのページへようこそ 上記のボタンから算数 割合の文章題ドリル(pdfプリント・問題集)がダウンロードできます。個人利用は無料です(家庭以外での配布は有料です)。 プリント内の数字はランダムです。


2



文字式 割合 パーセント の問題をわかりやすく解く方法 数スタ
・倍を表す数を分数で表す場合があることを知る。 知・技2つの数量の倍関係を表す数が分数となる場合があることを理解している。 12 割合が分数で表されているときも,比較量や基準量を求めることができる。



帯分数の計算方法 足し算 引き算 掛け算 割り算 小学生への教え方のポイント 数学fun



1 3 さんぶんのいち を1 2 にぶんのいち よりも大きいと捉えてしまう はる先生のさんすう教室 Ld 算数障害の子どものための動画授業


2
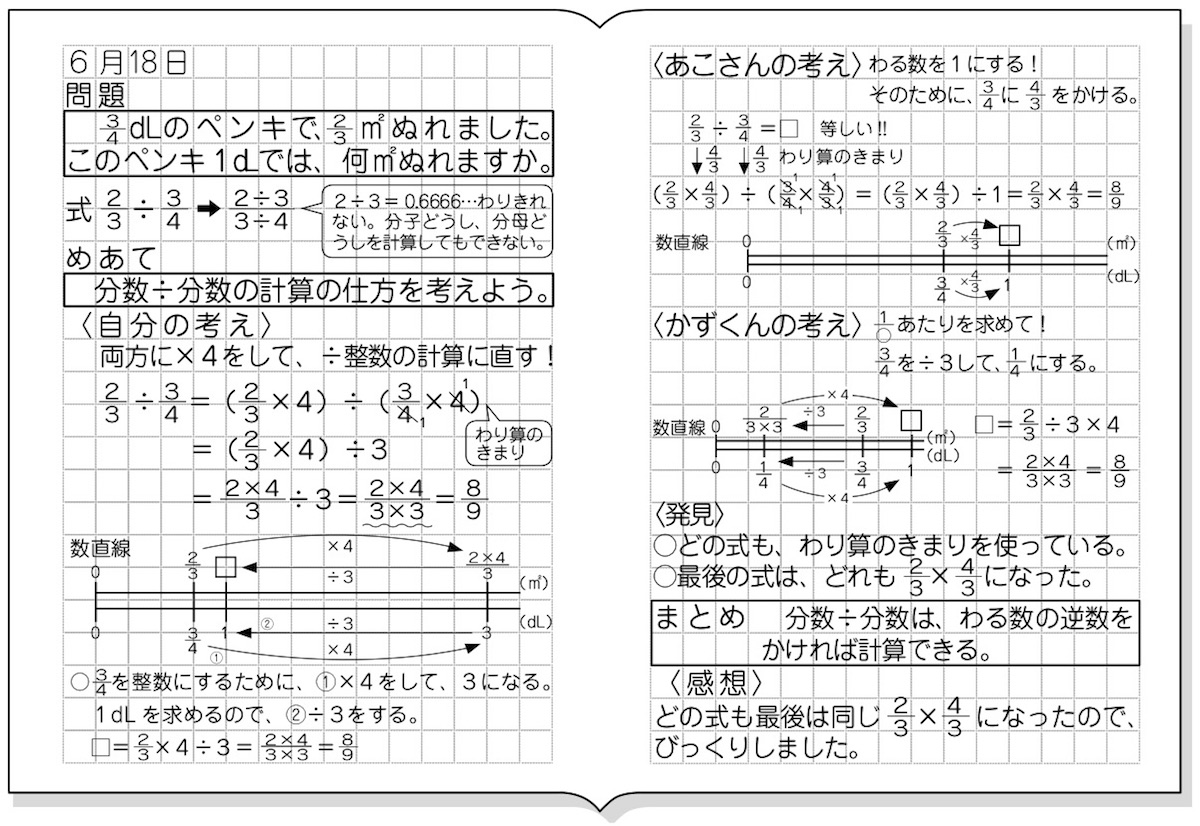


小6算数 分数のわり算 指導アイデア みんなの教育技術


2



Amazon Co Jp Learneasy 割合ポスター割合を学ぼう 分数 小数 百分率 歩合 大判a2サイズ 一覧表 小学生算数教材 おもちゃ


Http Www Sankyouken Jp Articles Download 226


Http Www Zkai Co Jp Jr K Mihon 1m Ouyou Pdf


Http Ousar Lib Okayama U Ac Jp Files Public 5 Papyrus 022 056 065 Pdf


Http Www Ginowan Okn Ed Jp Userfiles File 0619sueyoshi Pdf



50 グレア割合 を 表す 分数


2


Http Www Kochinet Ed Jp Shimizu E Kounaikensyuu H28sidouan6nen Pdf



求め方教えてください Clear



文字式 分数の計算問題を1から丁寧に 数スタ


Http Www Torikyo Ed Jp Kyoiku C H29ad 04 3 Pdf



新しい算数 2年度用 小学校教科書のご紹介 東京書籍



小5 算数 小5 37 分数の技 時間と分数編 Youtube


Http Mikawaya Sub Jp T2 Math Sansu Kyoiku 16 6 Pdf


Www Pref Miyagi Jp Uploaded Attachment Pdf


2


Www Edu City Yokohama Lg Jp Sch Kenkyu Es Sansu Pdf R1 Teian R195 Pdf


Www Shiga Ec Ed Jp Www Contents Html Common Other 5f6db0d3084 Pdf


Http Www Kochinet Ed Jp Ashizurimisaki E 11 27 3 4nennsidouann Pdf


2


Http Www Impuls Tgu Org Cms Templates File Php Url 2fcms 2flibrary Pdf Files 2f123 2fyamanashi Pdf



小学校5年生が考案して話題 分数ものさし は小学生のつまづきをどう解消する ほんのひきだし


2



ベストコレクション 割合 を 表す 分数 リタ ベルナル


6年生算数科に関する教材研究 野小ニュース6号 野原小学校



小数の割合 百分率 Youtube



分数を小数に直すには 分数の計算でよく使う 基本知識 で簡単に理解しよう 中学受験ナビ



メルカリ 小6算数 分数のわり算 問題56ページ分 スモールステップで学力アップ 参考書 444 中古や未使用のフリマ


Www Wakayama Wky Ed Jp Nagusa Wp Content Uploads Sites 52 16 01 562efd90a804d2a03d2 Pdf



ベスト 小学校 5 年生 算数 割合 Fuutou Sozai



積分定数 T Co Khm2swadv0 足し算のできる分数は量分数です この例の場合は割合分数であり 割合分数は内包量なので 足し算はもともとできないのです 割合分数 と 量分数 この2つの違いをきちんと教えることが大切です T



ヤフオク 単行 算数教育の理論と実践 数学教育学研究会


Http Eio Shimane Jp Files Original de5cbdeb Pdf



あの 縮図のやつで 何分の一ですか っていう問題が苦手です Clear


Www Pref Saitama Lg Jp G24 Expert Documents Shidouan Shou Sannsu Pdf


Core Ac Uk Download Pdf Pdf



分数 分数 分数のわり算を使って 03 割合を表す分数 Youtube


Www Pref Saitama Lg Jp G24 Expert Documents Shidouan Shou Sannsu Pdf


2



18年4月19日 算数 割合 概数と整数と分数 オンライン家庭教師 ウェブリー



小学校5年生算数 割合を表すグラフ



分数をかける計算 分数のかけ算を使って 01 割合を表す分数 Youtube



濃度算の解き方 大人の学び直し算数 計算のやり方解説 無料



印刷可能無料 算数 割合 デザイン文具



すきるまドリル 小学5年生 算数 割合と百分率 無料学習プリント すきるまドリル 無料学習プリント


Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Cc100 Sannsuu Documents S5 018 Pdf



小5 算数 小5 47 割合と百分率 編 Youtube


Www Nipponhyojun Co Jp Sansuu Jugyou Dvd Sansu No Jugyo Pdf



5年生算数 分数 黒板log 黒板log


2


2


Http Ousar Lib Okayama U Ac Jp Files Public 5 Papyrus 022 056 065 Pdf


Http Ypir Lib Yamaguchi U Ac Jp Bg File 1635 Bga Pdf



小学校5年生が考案して話題 分数ものさし は小学生のつまづきをどう解消する ほんのひきだし


2
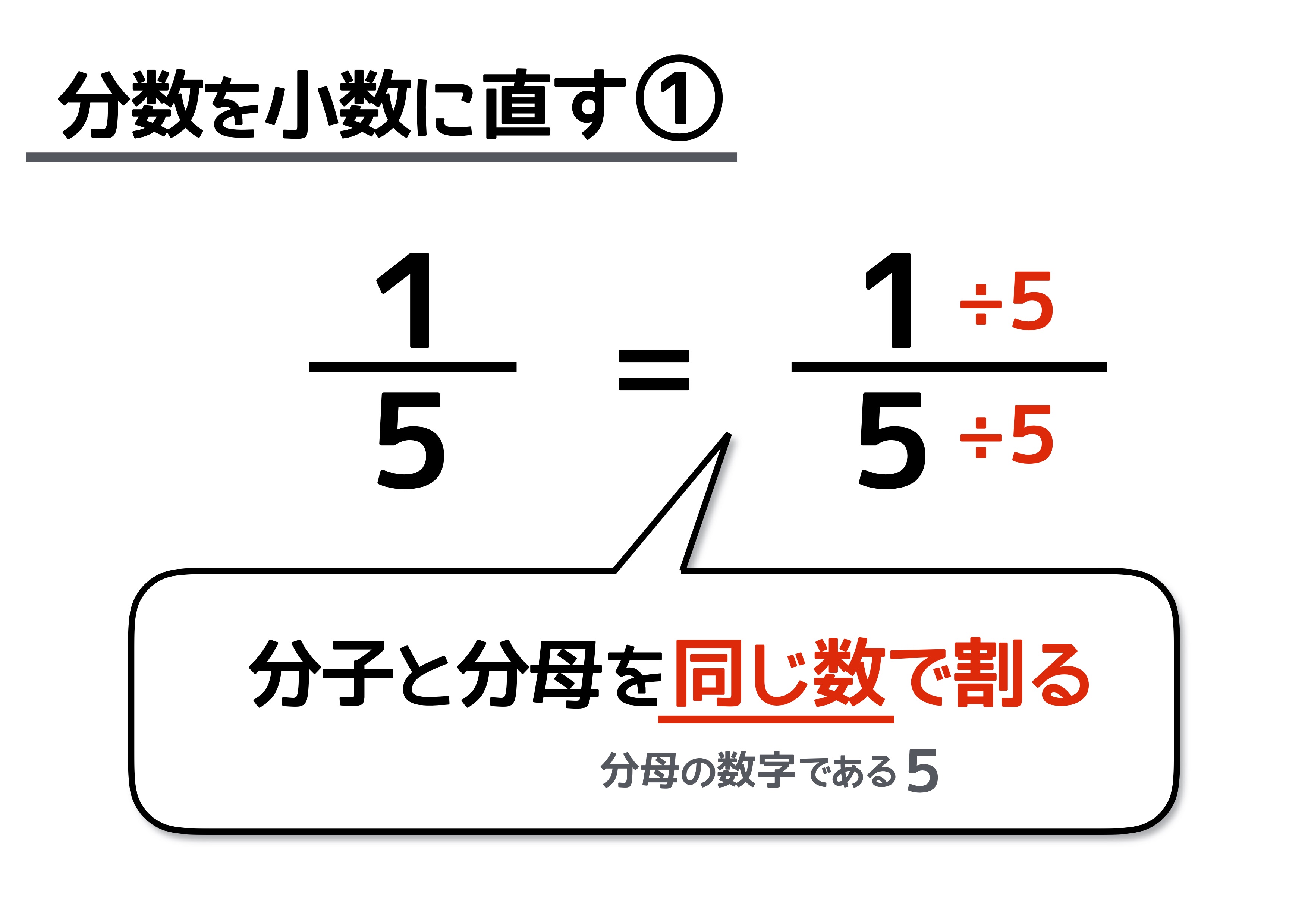


分数を小数に直すには 分数の計算でよく使う 基本知識 で簡単に理解しよう 中学受験ナビ


Www Pref Saitama Lg Jp G24 Expert Documents Shidouan Shou Sannsu Pdf



小数のわり算 割合を表す小数 01 Youtube



分数 分数 分数のわり算を使って 01 割合を表す分数 Youtube
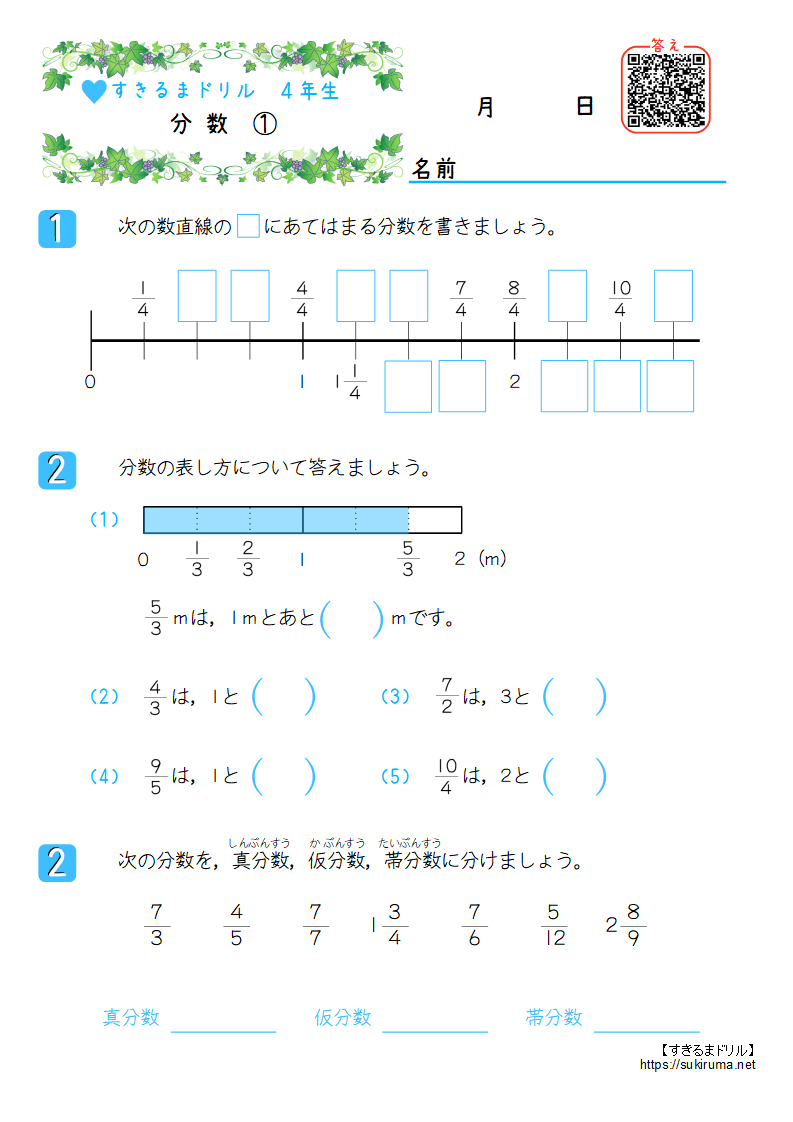


すきるまドリル 小学4年生 算数 分数 無料学習プリント すきるまドリル 無料学習プリント



新しい算数 2年度用 小学校教科書のご紹介 東京書籍



連立方程式 割合の問題 おっかぁ Note


2



小5 算数 小5 28 わり算と分数 倍編 Youtube


Http Www Hyogo C Ed Jp Gimu Bo Gakuryokutyousa Kadai H28 03 28a92 Pdf


2
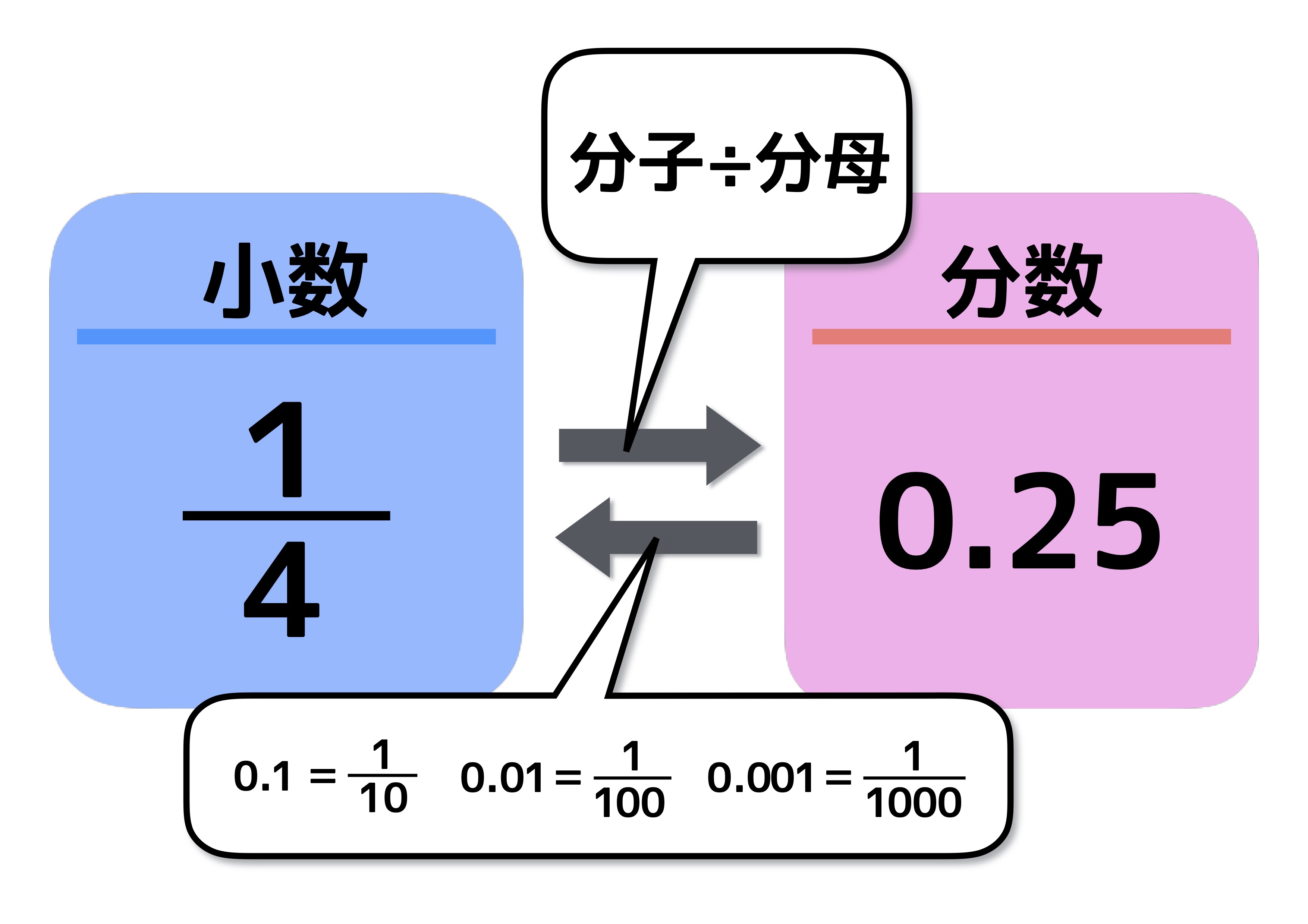


分数を小数に直すには 分数の計算でよく使う 基本知識 で簡単に理解しよう 中学受験ナビ



分数のかけ算 わり算 分数 整数 分数 整数 無料で使える学習ドリル



すきるまドリル 小学3年生算数 分数 無料学習プリント すきるまドリル 無料学習プリント


2


2


Http Www1 Iwate Ed Jp Db Db2 Sid Data Es Hukushiki R01 Esfu Pdf



新しい算数 2年度用 小学校教科書のご紹介 東京書籍


分数のたし算は何故通分するの フリースペースやすらぎの森の一日



小学校5年 算数 小数を分数であらわす Youtube


Http Www C Niiza Ed Jp E Katayama Pdf Kenkyu Kenkyu22 3nensansu Suizuki Pdf
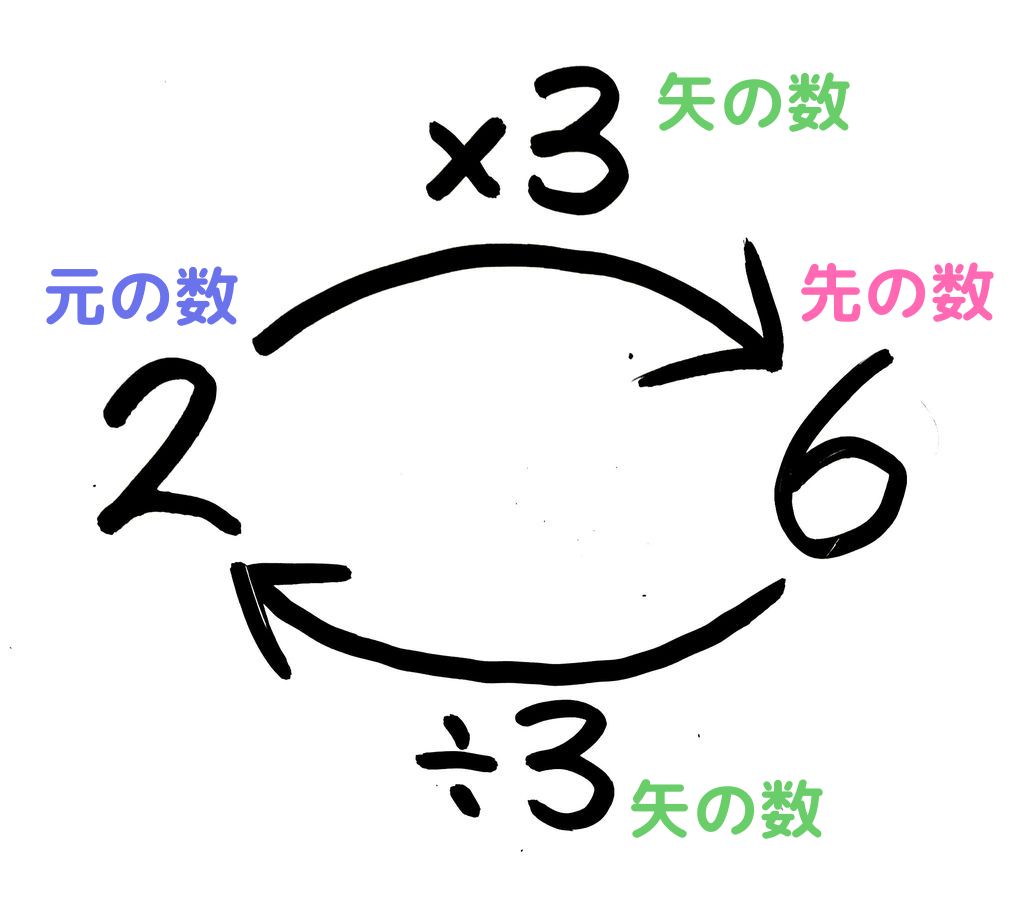


小学5年生 割合の簡単な求め方は くもわ 公式より分かりやすい出し方 そうちゃ式 分かりやすい図解算数 旧館


Www Pref Tottori Lg Jp Secure E Sansuu5 2 Pdf



新しい算数 2年度用 小学校教科書のご紹介 東京書籍



割合の単位 大人の学び直し算数 計算のやり方解説 無料



強育ドリル 完全攻略 分数 考える力を育てる 宮本 哲也 本 通販 Amazon



0 件のコメント:
コメントを投稿